Question

Using the image below, determine the equation of the circle.

Answer 1

-The equation for the following problem:

`(x+2)^2+(y-1)^2= 9`

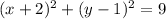
Explanation:

-The equation of a circle:

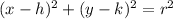`(x-h)^2+(y-k)^2=r^2` (where
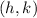`(h,k)` represents the center and
`r` represents the radius).

-According to following circle on a graph, the center of the circle is
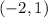`(-2,1)` and to find the radius you need to use the center and the point on a circle, which I pick a coordinate
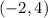`(-2,4)`, to solve the equation and get the radius:

`(-2+2)^2+(4-1)^2=r^2`

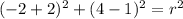
Solve:

`(-2+2)^2+(4-1)^2=r^2`

`0+(3)^2=r^2`

`0+9 = r^2`

`9 = r^2`

`√(9) = √(r^2)`

`3 = r`

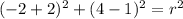
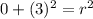
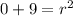
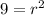
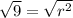
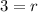
-So, after you found the radius, use the center and the radius to make the equation of a circle:

`(x+2)^2+(y-1)^2= 3^2`

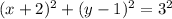
When putting the center and the radius on the equation of a circle, the radius needs to be simplified by the exponent and now you have found the answer for the following circle on a graph:

`(x+2)^2+(y-1)^2= 9`

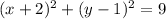
-There is one trick to get the center and the radius, look at the center of the circle if you see the coordinate that is in middle, then that would be the coordinate for the center, which is
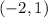`(-2,1)`. To find the radius, count from the center, which is coordinate
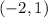`(-2,1)` to a point that lands on a circle, which is
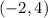`(-2,4)`. Since the distance is
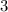`3`, simplify the
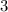`3` by the exponent
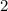`2`, because the radius is
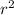`r^2` from the equation of a circle and you get the radius
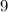`9`.

Answer 2

Circle Formula : ( x + 2 )^2 + ( y - 1 )^2 = 9; Option A

Explanation:

Applying circle formula ( x - a )^2 + ( y - b )^2 = r^2, for r ⇒ radius, around center point ( a, b );

We can determine the circle equation through the identification of this circle's center, and from then we can find the radius, square it etc.

Center of Circle ⇒ ( - 2 , 1 )

Radius ⇒ 3 units

Knowing this, substitute the values of the center points and r into the basic circle formula;

( x - ( - 2 ) )^2 + ( y - 1 )^2 = ( 3 )^2,

* Circle Formula : ( x + 2 )^2 + ( y - 1 )^2 = 9 *