Question

What is the correct order of the functions from least to greatest according to the average rate of change on the interval from x = -1 to x =3?

Answer 1

g(x) , f(x) , h(x)

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one.

Please have a look at the attached photo.

My answer:

As we all know, the average of change can be determined by the following formula:

`(f(b)-f(a))/(b-a)`

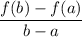
• As can be seen in the attached photo, The function f(x) is given by:

`f(x)=(x+3)^2-2`

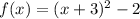
x = -1 we have:

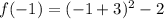`f(-1)=(-1+3)^2-2` = 2

x = 3 we have:

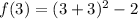`f(3)=(3+3)^2-2` = 34

Hence,the average rate of change of f(x) is:

`(34-2)/(3-(-1)) = 8`

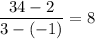
• As can be seen in the attached photo, The function g(x) is a straight line that passes through: (-1,-2) and (3,0)

<=> when x = -1 y = -2 and when x = 3 y = 0

=> the average rate of change of g(x) is:

`(g(3)-g(-1))/(3-(-1)) = (1)/(2)`

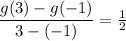
• Based on the table of values of h(x) we have:

h(-1)= 14

h(3)= 62

=> the average rate of change of h(x) is:

`(62-14)/(4) = 12`

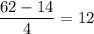
Therefore, the correct order of the functions from least to greatest according to the average rate of change is: g(x) , f(x) , h(x)

Hope it will find you well.