Question

What is the arc measure of ABC in degrees?

with

(20y - 11)

(4y +6) AP

(7y - 7)

Answer 1

Arc measure of ABC is 283°

Explanation:

We know the total angle of the circle is 360°.

Therefore,

(20y - 11) + (4y +6) + (7y - 7) = 360°

Collecting like terms, we have:

20y + 4y + 7y = 360 + 7 - 6 + 11

31y = 372

Let's divide both sides by 31.

`(31y)/(31) = (372)/(31)`

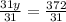
y = 12

The arc measure of ABC is the sum of AB and BC. To find the arc measure of ABC, we have:

(4y +6) + (20y - 11)

Collecting like terms, we have:

4y + 20y + 6 - 11

24y - 5

Let's substitute 12 for y

24(12) - 5

288 - 5 = 283°

Arc measure of ABC is 283°

Answer 2

The measure of arc ABC is 283°.

Explanation:

We know that the whole arc is equal to 360°, that means

`AC+AB+BC=360`

Where
`AC=7y-7`,
`AB=4y+6` and
`BC=20y-11`. Replacing these expressiones, we have

`7y-7+4y+6+20y-11=360\\31y-12=360\\31y=360+12\\y=(372)/(31)\\y=12`

But, arc ABC is defined by the sum of arcs AB and BC:

`ABC=AB+BC=4y+6+20y-11=24y-5=24(12)-5=283`

Therefore, the measure of arc ABC is 283°.