Answer:
the positive slope of the asymptote = 5
Explanation:
Given that:
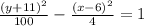
Using the standard form of the equation:
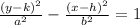
where:
(h,k) are the center of the hyperbola.
and the y term is in front of the x term indicating that the hyperbola opens up and down.
a = distance that indicates how far above and below of the center the vertices of the hyperbola are.
For the above standard equation; the equation for the asymptote is:
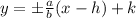
where;
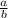 is the slope
is the slope
From above;
(h,k) = 11, 100
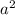 = 100
= 100
a =
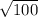
a = 10
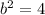
b =
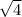
b = 2
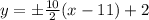
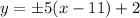
y = 5x-53 , -5x -57
Since we are to find the positive slope of the asymptote: we have
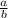 to be the slope in the equation
to be the slope in the equation
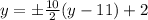
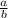 =
=
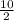
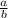 = 5
= 5
Thus, the positive slope of the asymptote = 5