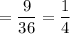Answer:

Explanation:
When you roll two fair cubes once, the outcomes are given below:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
Total Number of Outcomes=36
The sum of the outcomes less than 7 are:
2,3,4,5,6
3,4,5,6
4,5,6
5,6
6
Number of Even sum less than 7=9
Therefore:
Probability of getting an even sum less than 7