Question

What is the maximum number of possible extreme values for the function,

f(x) = х2 + 4х2 – 3х – 18 ?

Answer 1

(0.3, -18.45).

Explanation:

We need to recur to the extreme value theorem, which states: "If a function is continuous on a closed interval, then that function has a maximum and a minimum inside that interval".

Basically, as the theorem states, if a dunction is continuous, then it has maxium or minium.

In this case, we have a quadratic function, which is a parabola. An important characteristic of parabolas is that they have a maximum or a minium, but they don't have both. When the quadratic term of the fuction is positive, then it has a minium at its vertex. When the quadratic term of the function is negative, then it has a maximum at its vertex.

So, the given function is
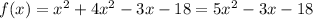`f(x)=x^(2) +4x^(2) -3x-18=5x^(2) -3x-18`, where the quadratic term is positive, so the functions has a minimum at
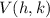`V(h,k)`, where
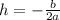`h=-(b)/(2a)` and
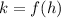`k=f(h)`, let's find that point

`h=-(-3)/(2(5)) =(3)/(10) =0.3`

`k=f(0.3)=5(0.3)^(2) -3(0.3)-18=0.45-0.9-18=-18.45`

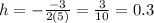
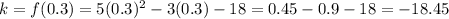
Therefore, the minium of the function is at (0.3, -18.45).