Answer:
Sequence :
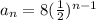
Rate of change : -3
Explanation:
It is given that the sequence represents by the points (1,8), (2,4), (4,1) and (5,0.5).
We know that the
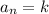 represent the point (n,k). So, we have
represent the point (n,k). So, we have
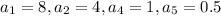
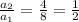
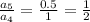
It is clear that the above sequence is a geometric sequence because it has common ratio
 .
.
First term :

Common ratio :
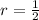
The nth term of a G.P. is
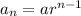
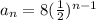
Therefore, the required sequence is
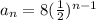 .
.
We need to find the average rate of change from n = 1 to n = 3.
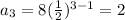
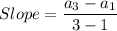
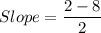
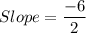

Therefore, the average rate of change from n = 1 to n = 3 is -3.