Question

Solve the quadratic equation by completing the square.
x^2+12x+52=0

Answer 1

(x + 6)² + 16 = 0

Explanation:

To complete the square we will first need to get our equation to look like: x² + bx = c

Here we have x² + bx + c = 0 → x² + 12x + 52 = 0

• First we need to subtract our c, in this case 52, from both sides to get x² + 12x = -52
• We then need to add
  `((b)/(2) )^(2)` to both sides of the equation
• Here our b value is 12, so plugging this into our formula we get
  `((12)/(2) )^(2) =(6)^(2) =36`
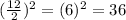
• Adding 36 to both sides our equation becomes: x² + 12x + 36 = -52 + 36
• Then combining like terms on the right side we get x² + 12x + 36 = -16
• Now making our left side of the equation into a perfect square we get: (x + 6)² = -16
• Finally adding the 16 to both sides of the equation we get: (x + 6)² + 16 = 0