Answer:
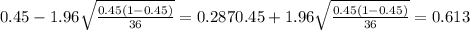
we can conclude at 95% of confidence that the true proportion of interest for this case is between 0.287 and 0.613
Explanation:
The estimated proportion of interest is
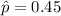
We need to find a critical value for the confidence interval using the normla standard distributon. For this case we have 95% of confidence, then the significance level would be given by
 and
and
 .
.
And the critical value is:
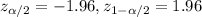
The confidence interval for the true population proportion is interest is given by this formula:
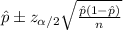
Replacing the values provided we got:

And we can conclude at 95% of confidence that the true proportion of interest for this case is between 0.287 and 0.613