Question

Which points are the approximate locations of the foci of the ellipse? Round to the nearest tenth. (−2.2, 4) and (8.2, 4) (−0.8, 4) and (5.2, 4) (3, -1.2) and (3, 9.2) (3, 1.3) and (3, 6.7)

Answer 1

A

Explanation:

took quiz

Answer 2

The graph is attached.

Answer:

(-2.2, 4) and (8.2, 4)

Explanation:

In an ellipse, there is a minor radius and a major radius.

Let major radius be = a

Let minor radius be= b

From the graph, we are given:

Major radius, a = 6

Minor radius, b = 3

Now, let's find the distance from the center to the focus using the formula:

`√(a^2 - b^2)`

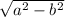
Substituting values, we have:

`= √(6^2 - 3^2)`

`= √(36 - 9)`

`= √(27) = 5.916`

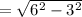
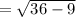
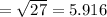
≈ 5.2

We can see from the graph that center coordinate is (3, 4). Therefore, the approximate locations of the foci of the ellipse would be:

(3-5.2, 4) and (3+5.2, 4)

= (-2.2, 4) and (8.2, 4)