Question

Write the equation of a line that is perpendicular to y = -0.3z +6 and that passes through the point

(3,–8).

Answer 1

y = 3.33x - 18

Explanation:

In order for a line to be perpendicular to another, it must have a slope with the negative reciprocal

• Here in the equation y = -0.3z + 6 has a slope of -0.3 (can also be written as
  `-(3)/(10)`)
• A line that is perpendicular to this line will need to have a slope of 3.33 repeating (or
  `(10)/(3)`)
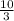• I will using fractions for simplicity and convert to decimals afterwards

Since we have our slope and the two points, we can plug them into y = mx + b to solve for b and write our new equation of a line

• Substituting in the values that we have we get:
  `-8=(10)/(3)(3)+b`
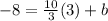
• Simplifying we get -8 = 10 + b, making b = -18

Now that we have our slope and our y-intercept we can plug them into the same formula used before to find our perpendicular line:

• 
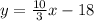  `y= (10)/(3)x-18` which can also be written as y = 3.33x - 18