Answer:
The correct answer to the following question will be "
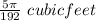 ".
".
Explanation:
Give that the volume of the box = xyz cubic feet
Amount of jars which you can make =
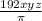
Let the volume of the removed clay = V cubic feet
As we know,

As we place the values in the equation above, we obtain
⇒
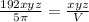
When multiplication is applied we receive
⇒
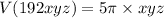
⇒
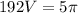
⇒
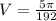 cubic feet
cubic feet