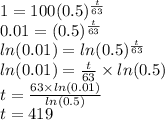Question

Radioactive isotope #1

has been kept for 3.3 years. Originally, there were 100 grams and now there are 96.43 grams.

What is the half-life?
Round to the nearest year
What is the mystery element?
When will there be 1 gram left?
Round to the nearest year

Answer 1

Half-life = 63 years

Mystery element is Titanium-44

There will be 1 gram left after 419 years have passed

Explanation:

In general the equation describing half-life is:

`m=m_0 (0.5)^{\frac {t}{t_(1/2)}`

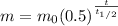
Where m is the final mass, m0 is the starting mass, t is the total elapsed time, and t(1/2) is the length of the half life. t / t(1/2) is actually the number of half-lives that have passed.

Anyways - all your questions can be answered using the above equation.

What is the half-life?

I subbed in the values we know from the question. In solving this I used the natural logarithm (but a log of any base will do - the goal is to bring down the exponent):

`96.43=100(0.5)^(3.3)/(t_(1/2))\\0.9643=(0.5)^(3.3)/(t_(1/2))\\ln(0.9643)=ln(0.5)^(3.3)/(t_(1/2))\\ln(0.9643)=(3.3)/(t_(1/2)) * ln(0.5)\\t_(1/2) =(3.3)/(ln(0.9643)) * ln(0.5)\\t_(1/2) = 63`

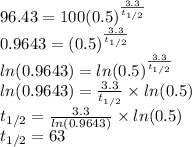
What is the mystery element?

Titanium-44, because it's half-life in the table is closest to the calculated half-life.

When will there be 1 gram left?

Again use the equation. This time the total time, t, is unknown. We can use the previously calculated half-life:

`1=100(0.5)^(t)/(63)\\0.01=(0.5)^(t)/(63)\\ln(0.01)=ln(0.5)^(t)/(63)\\ln(0.01)=(t)/(63) * ln(0.5)\\t=(63 * ln(0.01))/(ln(0.5))\\t=419`