Question

Why does it make sense that the equation includes the term 0.05 0.05 12? That is, why are we

dividing 0.05 by 12?

Answer 1

Corrected Question

Most savings accounts advertise an annual interest rate, but they actually compound that regular intervals during the year. That means that if you own an account, you'll be paid a portion the interest before the year is up, and, if you keep that payment in the account, you will start an interest on the interest you have already earned. For example, suppose you put $500 in a savings account that advertises 5% annual interest if that interest is paid once per year, then your balance B after years could be computed using the equation
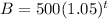`B = 500(1.05)^t`. since you'll end each year with 100% + 5% of the amount you began the year with.

On the other hand, if that same interest rate is compounded monthly, then you would compute your balance after t years using the equation:

`B = 500 (1 +(0.05)/(12) )^(12t)`

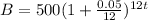
a. Why does it make sense that the equation 0.05 by 12?

b. How does this equation reflect the fact that you opened the account with $500?

c. What does the "12t" in the equation represent?

Answer:

See Explanation

Explanation:

(a)For an interest compounded periodically, the interest rate is divided by the number of periods.

Since the interest is compounded monthly, the interest rate 0.05 is divided by 12.

(b)In the compound interest formula

Amount
`B=P(1+(r)/(k))^{nk`

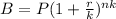
P is the initial amount in the account.

Comparing with:
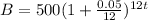`B = 500 (1 +(0.05)/(12) )^(12t)` , our starting amount, P=$500.

(c)12t represents the number of times the investment is compounded in total. t is the number of years for which the principal is invested.

Since it is compounded monthly, we multiply t by 12.