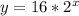Question

Write an exponential function in the form y=ab^xy=ab x

that goes through points (0, 16)(0,16) and (7, 2048)(7,2048).

Answer 1

`y = 16*2^(x)`

Explanation:

For this case we have two points given (0,16) and (7,2048). And we want to find a function given by this general expression:

`y= ab^x`

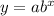
And using the first point given we have:

`16 = a b^0 a = 16`

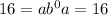
Now we can use the info from the second point and we have:

`2048 = 16 b^7`

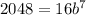
We can divide 16 in both sides and we got

`128=b^7`

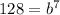
And using an exponent 1/7 in both sides we got:

`(128)^(1/7) = b b = 2`

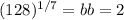
And then our model would be given:

`y = 16*2^(x)`

Answer 2

`y = 16*2^(x)`

Explanation:

We want an exponential function in the following format:

`y = ab^(x)`

Goes through the point (0,16).

This means that when
`x = 0, y = 16`

So

`y = ab^(x)`

`16 = ab^(0)`

Since
`b^(0) = 1`

`a = 16`

So

`y = 16b^(x)`

Goes through the point (7,2048).

This means that when
`x = 7, y = 2048`

Then

`y = 16b^(x)`

`2048 = 16b^(7)`

`b^(7) = (2048)/(16)`

`b^(7) = 128`

`b = \sqrt[7]{128}`

`b = 2`

So the function is:

`y = 16*2^(x)`