Question

Write an equation for a rational function with: vertical asymptotes at -1 and 4 x intercepts at 6 and 3 and a y intercept at 7

Answer 1

`f(x)=-(14(x-3)(x-6))/(9(x+1)(x-4))`

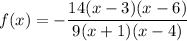
Explanation:

The vertical asymptotes will be found where the denominator is zero. The x-intercepts will be found where the numerator is zero. The y-intercept can be made what you like using a suitable vertical scale factor.

Denominator factors: (x+1), (x-4) . . . . make the vertical asymptotes

Numerator factors: (x-6), (x-3) . . . . make the x-intercepts.

Now, our function is ...

f(x) = a(x -6)(x -3)/((x +1)(x -4))

The y-intercept for this is ...

f(0) = a(-6)(-3)/(1(-4)) = a(-18/4) = -9a/2

We want to choose "a" so this is 7:

7 = -9a/2

-14/9 = a . . . . multiply by -2/9

The rational function you want is ...

`\boxed{f(x)=-(14(x-3)(x-6))/(9(x+1)(x-4))}`