In a right-angled triangle with a height of 3 and a hypotenuse of
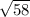 , the angle x is approximately 22 degrees.
, the angle x is approximately 22 degrees.
In a right-angled triangle, the relationship between the sides is given by the Pythagorean theorem:

where a and b are the legs of the right triangle and c is the hypotenuse.
In your case, the height (a) is given as 3, and the hypotenuse (c) is given as
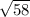 .
.
So, the equation becomes:
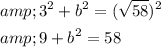
Now, solve for b:
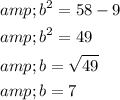
Now that you know the length of the other leg (b), you can find the angles using trigonometric ratios.
The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side. So, for the angle x:
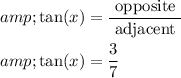
Now, find the angle x using the arctangent (inverse tangent) function:
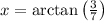
Use a calculator to find the arctangent of
 and round the result to the nearest degree. The answer should be approximately 22 degrees.
and round the result to the nearest degree. The answer should be approximately 22 degrees.
So, the correct option is 4. 22 degrees.