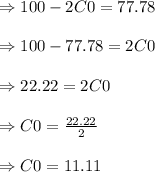Question

You are attempting to value a call option with an exercise price of $100 and one year to expiration. The underlying stock pays no dividends, its current price is $100, and you believe it has a 50% chance of increasing to $116 and a 50% chance of decreasing to $84. The risk-free rate of interest is 8%. Calculate the call option’s value using the two-state stock price model.

Answer 1

The answer is "11.11"

Step-by-step explanation:

Given values:

The chances of increasing value by 50% is = 116

The chances of decreasing value by 50% is = 84

So, the two possible stock prices are:

S+ = 116 and S- = 84

The exercise price is = 100 so, possible called value are

Chance of increase (Ci) = 116-100 = 16

Chance of decrease (Cd)= 84 -100 = -16 it is - value that's why we avoid this so it equal to 0.

Formula:

edge ratio =
`((Ci - Cd))/((S+ - S-))`

`= ((16 - 0))/((116 - 84)) \\\\=(16)/(32)\\\\= (1)/(2)\\\\= 0.5`

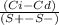
To develop a risk-free makes the image of one stock share and dual calling in paper. The actual cost of risk-free image is = exercise price- 2C0

= 100 -2C0

= 84 after some years.

The given value is = 84

time = 1 year

interest rate= 8%

interest:

`= (84)/((1+0.08)^1) \\\\= (84)/(1.08) \\\\= (84)/((108)/(100)) \\\\ = (84 * 100)/(108)\\\\ = 77.78`

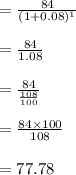
if the edged position is equivalent to the actual payout cost:

`\Rightarrow 100 - 2C0 =77.78 \\\\\Rightarrow 100 -77.78 = 2C0 \\\\\Rightarrow 22.22 = 2C0 \\\\\Rightarrow C0 = (22.22)/(2) \\\\\Rightarrow C0= 11.11`