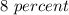Question

You purchased an annual interest coupon bond one year ago that had six years remaining to maturity at that time. The coupon interest rate was 10%, and the par value was $1,000. At the time you purchased the bond, the yield to maturity was 8%. If you sold the bond after receiving the first interest payment and the yield to maturity continued to be 8%, your annual total rate of return on holding the bond for that year would have been

Answer 1

The correct answer to the following question will be "8%".

Step-by-step explanation:

The given values are:

Number of years of maturity = 5 years

Interest rate of coupon = 10%

= 10%×1000

= 100

Yield to maturity, YTM = 8%

As we know,

Price of Bond = PV of Coupons + PV of Per Value

On putting the values in the above formula, we get

⇒ =
`(100* (1-(1+8 \ percent^(-5))))/(8 \ percent) +(1000)/(1+8 \ percent^(5))`

⇒ =
`1079.85`

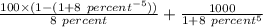
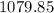
After 1 years, we get

Price of Bond = PV of Coupons + PV of Per Value

On putting the values in the above formula, we get

⇒ =
`(100* (1-(1+8 \ percent^(-4))))/(8 \ percent) +(1000)/(1+8 \ percent^(4))`

⇒ =
`1066.24`

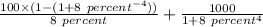
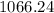
Now,

The total return rate =
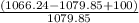
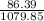
`((1066.24-1079.85+100))/(1079.85)`

=
`(86.39)/(1079.85)`

=
`8 \ percent`