Answer:
1) a) 45 seats; b) $ 40
2) 548 cases
3) a) 20; b) elastic; c) 8; d) elastic
Explanation:
1) Maximize profit
a) Number of seats to maximize profit
Let p = the profit per seat
and s = the number of seats
We have the conditions:
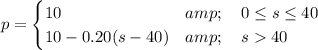
The total profit P is the number of seats times the profit per seat.
Thus, the total profit function is
![P = \begin{cases}10s & \quad 0 \leq s \leq 40\\s[10 - 0.20(s - 40)] & \quad s > 40\\\end{cases}](https://img.qammunity.org/2021/formulas/mathematics/college/xscjk4gwlma89jvrxdbj71bm76u8yg0lhf.png)
The equation for the function when s > 40 is
P = s[10 - 0.20(s - 40)] = s(10 - 0.20s + 8) = s(18 - 0.20s) = 18s - 0.20s²
This is the equation of a parabola.
In standard form,
P = -0.20s² + 18s
a = -0.20; b = 18; c = 0
The parabola opens downwards, because a < 0. Therefore, the vertex is a maximum.
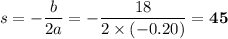
The maximum profit occurs at 45 seats.
b) Maximum profit
P = -0.20s² + 18s = -0.20×45² + 18×45 = -405 + 810 = 405
The graph below shows that the maximum profit is $405.
2. Number of lots to order
The number of cases to be ordered to maximize profit is the economic order quantity (q).
The formula is
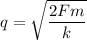
where
F = the fixed setup cost to manufacture the product
m = the total number of cases produced annually
k = the cost of storing one case for one year
Data:
F = $10/lot
m = 180 000 cases/yr
k = ($12/case)/yr
Calculation:
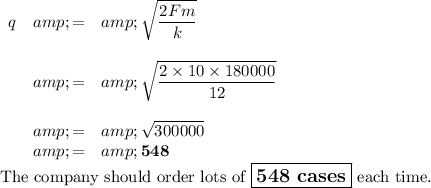
3) Elasticity of demand
Elasticity of demand (E) is an indicator of the impact of a price change on a product's sales.
The general formula for an exponential demand curve is
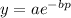
Your demand curve has the formula
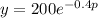
The formula for elasticity of demand is
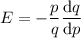
a) Elasticity at p = $50
The formula for elasticity at p = $50 is
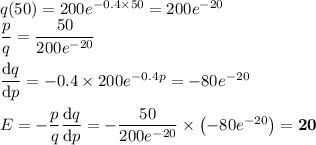
b) Meaning of E for p = $50
E > 1, so the demand is elastic.
If E = 20, a 1 % increase in price causes a 20 % decrease in demand.
c) Elasticity at p = $20
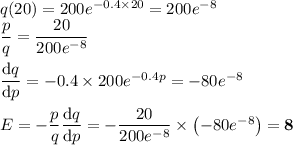
d) Meaning of E for p = $20
E > 1, so the demand is elastic.
If E = 8, a 1 % increase in price causes an 8 % decrease in demand.