Question

Suppose f(x)= INT(1,x^2) ((sin(t))/t)dt. What is f'(x)?

Answer 1

see below

Explanation:

The fundamental rule of calculus tells you that for ...

`\displaystyle f(x)=\int^(a(x))_b {u(t)} \, dt \\\\f'(x)=u(a(x))a'(x)-u(b(x))b'(x)`

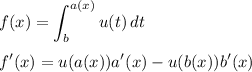
Then, for the specific case in this problem, we have ...

a(x) = x^2; a'(x) = 2x

b(x) = 1; b'(x) = 0

f'(x) = sin(x^2)/x^2·(2x)

f'(x) = 2sin(x^2)/x . . . . . matches choice D