Answer:
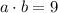
a x b = (-1,1,-1)
Explanation:
We can write the vectors a=(1,2,1) and b = (2,3,1), since given a vector of the form w = ci+dj+fk, its' components are (c,d,f).
The scalar (or dot) product of two vectors is obtained by multiplying each of the components of the two vectors and then summing up the results of each multiplication.
Then, in our case
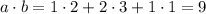
To calculate the vector product, we proceed as follows. First we form the matrix
![\left[\begin{matrix}i & j & k \\ 1 & 2 & 1 \\ 2 & 3 & 1 \end{matrix}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/pmsmbnt0ihnq6ooxd0cg304cg70l3xhokf.png)
And we calculate the determinant of this matrix(the explanation of 3x3 determinants is beyond the scope of this explanation). So, we get
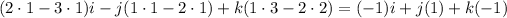
So a x b = (-1,1,-1).
To check that this is ok, we need to check that the scalar product between a x b and a is 0. Also it must happen that the scalar product a x b and b is 0.
Note that
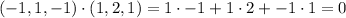

So a x b is correct