Answer:
99% of confidence intervals for mean age of ICU patients
(53.8920 , 61.2079)
Explanation:
Explanation:-
Given sample mean
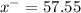
Given standard error is determined by
S.E =
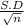
Given data standard error = 1.42
99% of confidence intervals for mean is determined by
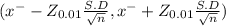
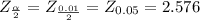
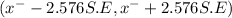
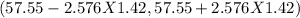
(53.8920 , 61.2079)
Conclusion:-
99% of confidence intervals for mean is determined by
(53.8920 , 61.2079)