Answer:
Prove set equality by showing that for any element
 ,
,
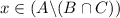 if and only if
if and only if
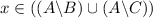 .
.
Example:
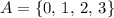 .
.
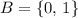 .
.
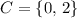 .
.
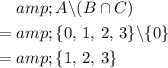 .
.
 .
.
Explanation:
Proof for
![[x \in (A \backslash (B \cap C))] \implies [x \in ((A \backslash B) \cup (A \backslash C))]](https://img.qammunity.org/2023/formulas/mathematics/high-school/evjkew9og2pyqz1jbct1udy9aci72zvfro.png) for any element
for any element
 :
:
Assume that
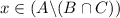 . Thus,
. Thus,
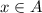 and
and
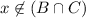 .
.
Since
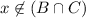 , either
, either
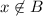 or
or
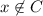 (or both.)
(or both.)
- If
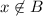 , then combined with
, then combined with
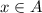 ,
,
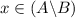 .
. - Similarly, if
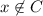 , then combined with
, then combined with
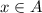 ,
,
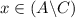 .
.
Thus, either
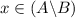 or
or
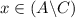 (or both.)
(or both.)
Therefore,
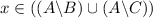 as required.
as required.
Proof for
![[x \in ((A \backslash B) \cup (A \backslash C))] \implies [x \in (A \backslash (B \cap C))]](https://img.qammunity.org/2023/formulas/mathematics/high-school/j9w09urpflumg7vg6f8ujgkvqoxxk2u0fd.png) :
:
Assume that
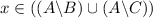 . Thus, either
. Thus, either
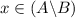 or
or
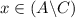 (or both.)
(or both.)
- If
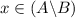 , then
, then
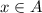 and
and
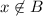 . Notice that
. Notice that
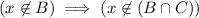 since the contrapositive of that statement,
since the contrapositive of that statement,
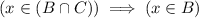 , is true. Therefore,
, is true. Therefore,
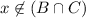 and thus
and thus
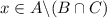 .
. - Otherwise, if
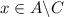 , then
, then
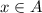 and
and
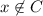 . Similarly,
. Similarly,
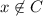 implies
implies
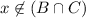 . Therefore,
. Therefore,
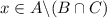 .
.
Either way,
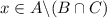 .
.
Therefore,
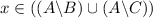 implies
implies
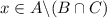 , as required.
, as required.