Question

Find the equation of a parabola with focus F(-1,-13) and directrix y=-9

Answer 1

We are asked to write the equation of parabola with focus
`F(-1,-13)` and directrix
`y=-9`.

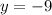Let us say that point (x,y) is on parabola.

We know that any point on parabola is equidistant from focus and directrix. Using distance formula we will get:

`√((y-(-9))^2)=√((x-(-1))^2+(y-(-13))^2)`

`√((y+9)^2)=√((x+1)^2+(y+13)^2)`

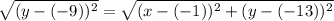
Square both sides:

`(y+9)^2=(x+1)^2+(y+13)^2`

`y^2+18y+81=(x+1)^2+y^2+26y+169`

`18y+81-81=(x+1)^2+26y+169-81`

`18y=(x+1)^2+26y+88`

`18y-26y=(x+1)^2+26y-26y+88`

`-8y=(x+1)^2+88`

`(-8y)/(-8)=((x+1)^2+88)/(-8)`

`y=-((x+1)^2)/(8)-11`

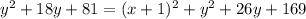
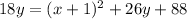
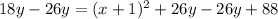
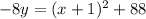
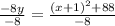
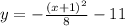
Therefore, our required equation would be
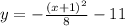`y=-((x+1)^2)/(8)-11`.