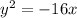Question

find the equation of the parabola P if it knows the coordinates of the focus F (-4.0) and the equation of the directrix x-4 = 0​

Answer 1

The equation is
`y^2=-16x`

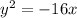
Explanation:

Since the directrix is a vertical line, we have that the parabola opens to the left or to the right. Then, the general equation of a parabola of this shape is

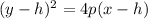`(y-h)^2 = 4p(x-h)` where (h,k) is the vertex of the parabola.

We know that the vertex of the parabola is the middle point of the distance between the Focus and the directrix of the parabola. To calculate the distance betweee the directrix and the focus, we will take a straight line that passes through the focus and is perpendicular to the directrix. In our case, this line is the x axis. Now, we see that this line intersects the directrix at the point (4,0). So, the middle point is given by the average of the coordinates of the two points (this is equivalent to summing up the coordinates and divide them by two. Then, the vertex is

`(h,k) = ((-4+4)/(2), (0+0)/(2)) = (0,0)`

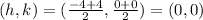
We only need to calculate the value of p. To do so, we know that the distance from the focus to the vertex is |p|. We can calculate this distance by using the distance formula. Recall that given two points (a,b), (c,d) the distance is given by
`\sqrt[]{(a-c)^2+(b-d)^2}`, so in this case

`|p| = \sqrt[]{(-4-0)^2+(0-0)^2} = 4`

We must define the value of p. Note that since the focus is on the left of the directrix, the parabola must open to the left. To guarantee that this happens, x must have a negative coefficient. Hence p = -4.

Then, the equation of the parabola is

`(y-0)^2 = 4(-4)(x-0)`

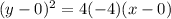
or
`y^2=-16x`