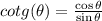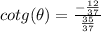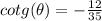Question

Given that sectheta = -37/12 what is the value of cottheta for pi/2 < theta< pi?

Answer 1

Explanation:

`sec(\theta) = (1)/(cos(\theta))`

`sec(\theta) = -(37)/(12)`

`(1)/(cos \theta) =-(37)/(12)`

`cos \theta =- (12)/(37)`

apply the following trigonometric identity

`sin \theta = √(1-cos^2\theta)\\\\sin\theta =\sqrt{1-((12)/(37))^2 }\\\\sin\theta=\pm \sqrt{(1225)/(1369) }\\\\sin\theta = (35)/(37)`

Therefore ,

`cot\theta =(cos\theta)/(sin\theta) =(-\\(12)/(37) )/((35)/(37) ) =-(12)/(35)`

for
`(\pi)/(2) <\theta<\pi`

Answer 2

`cotg(\theta) = -(12)/(35)`

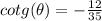
Explanation:

The cotangent of theta is:

`cotg(\theta) = (cos(\theta))/(sin(\theta))`

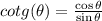
For pi/2 < theta< pi

This means that the angle is in the second quadrant. In the second quadrant, the cosine is negative and the sine is positive. This means that the cotangent will be negative.

Secant:

`sec(\theta) = (1)/(cos(\theta))`

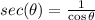
In this question

`sec(\theta) = -(37)/(12)`

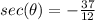
So

`-(37)/(12) = (1)/(cos(\theta))`

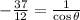
Using cross multiplication

`-37cos(\theta) = 12`

`37cos(\theta) = -12`

`cos(\theta) = -(12)/(37)`

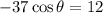
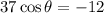
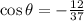
Now we apply the following trigonometric identity:

`sin(\theta)^(2) + cos(\theta)^(2) = 1`

`sin(\theta)^(2) + (-(12)/(37))^(2) = 1`

`sin(\theta)^(2) = 1 - (-(12)/(37))^(2)`

`sin(\theta)^(2) = 1 - (144)/(1369)`

`sin(\theta)^(2) = (1369 - 144)/(1369)`

`sin(\theta) = \pm \sqrt{(1225)/(1369)}`

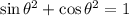
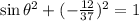
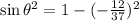
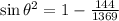
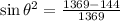
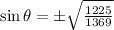
Since the angle is in the second quadrant, the sine is positive.

`sin(\theta) = (35)/(37)`

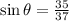
Finally, the cotangent:

`cotg(\theta) = (cos(\theta))/(sin(\theta))`

`cotg(\theta) = (-(12)/(37))/((35)/(37))`

`cotg(\theta) = -(12)/(35)`