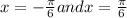Answer:
The general solution of
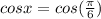 is
is
x = 2nπ±
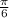
The general solution values
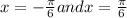
Explanation:
Explanation:-
Given equation is
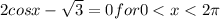
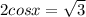
Dividing '2' on both sides, we get
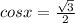
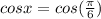
General solution of cos θ = cos ∝ is θ = 2nπ±∝
Now The general solution of
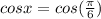 is
is
x = 2nπ±
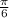
put n=0
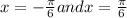
Put n=1
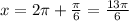
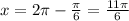
put n=2
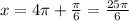
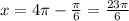
And so on
But given 0 < x< 2π
The general solution values