Question

the probability that we encounter a green light at the corner of college and main is 0.35, a yellow light 0.04, and a red light 0.61. whats the probability you will hit a green light on monday and a red light on tuesday

Answer 1

21% probability you will hit a green light on monday and a red light on tuesday

Explanation:

When two events, A and B, are independent, we have that:

`P(A \cap B) = P(A) * P(B)`

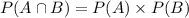
In this problem, we have that:

Event A: Green light on monday.

Event B: Red light on tuesday.

The probability that we encounter a green light at the corner of college and main is 0.35

This means that
`P(A) = 0.35`

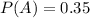
The probability that we encounter a red light is 0.61:

This means that
`P(B) = 0.61`

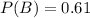
These events are independent, that is, the light color on Tuesday is independent of the color on Monday. So

`P(A \cap B) = P(A) * P(B) = 0.35 * 0.6 = 0.21`

21% probability you will hit a green light on monday and a red light on tuesday