Question

The area of the square, the

A cone fits inside a square pyramid as shown. For every


cross section, the ratio of the area of the circle to the area of


the square is on


Since the area of the circle is


volume of the cone equals


o


the volume of the pyramid or (2nch or arh.


Cross section


the volume of the pyramid or {27% (mor ar?h.


ce the volume of the pyramid or i ( 20?m) or

ỉ the volume of the pyramid or # (c2n?cm) or <.n?h.


the volume of the pyramid


Next


Save and Exit


Submit


Mark this and return

Answer 1

B.

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one.

Please have a look at the attached photo.

My answer:

As given in the question, we know that:

The ratio of the area of the circle to the area of the square is π/4

• The formula to find the volume of the cone is:

V = 1/3*the height*the base area

<=> V1 = 1/3*h*π
`r^(2)`

• The formula to find the volume of the pyramid is:

V2 = 1/3*the height*the base area

<=> V = 1/3*h*4
`r^(2)`

=> the ratio of volume of the cone to the pyramid is:

=
`(V1)/(V2)`

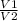
= (1/3*h*π
`r^(2)` ) / ( 1/3*h*4
`r^(2)` )

= π/4

S we can conclude that the volume of the cone equals π/4 the volume of the pyramid

Hope it will find you well.