Answer:
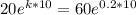
We can divide both sides by 20 and we got:

Now we can appply natural log on both sides and we got:
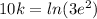
Now we can divide both sides of the equation by 10 and we got:
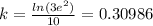
So then the aproximate value of k is 0.30986 and rounded would be 0.31
Explanation:
We have the following two expression:
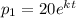
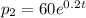
We know that the two populations were equal 10 years after the start of the study, so then we can create the following equation:
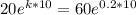
We can divide both sides by 20 and we got:

Now we can appply natural log on both sides and we got:
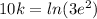
Now we can divide both sides of the equation by 10 and we got:
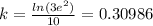
So then the aproximate value of k is 0.30986 and rounded would be 0.31