Answer:
A. (-11,0) and (11,0)
Explanation:
The given equation is
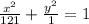
Where
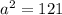 and
and
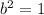 . Remember, the greater denominator is the parameter
. Remember, the greater denominator is the parameter
 .
.
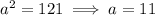

Now, the vertices of an ellipse with center at the origin are defined as
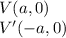
Replacing values, we have
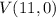 and
and
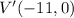
Therefore, the right answer is A.
(The image attached proves this result).