Question

What is the slope-intercept equation of the line below?

Answer 1

The slope-intercept form:

`y = -3x +4`

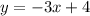
Explanation:

-To get the slope-intercept equation, you first need to find the slope by using this equation
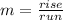`m = (rise)/(run)` (starting counting from the first point, to the second point) in order to get the slope. After you have the slope, you need to find the y-intercept ( y-intercept is where the line crosses the y axis of the graph, basically). So, to find that, you need look for the point that only crosses the y axis to get the y-intercept. After you have both the slope and y-intercept, you put it in slope-intercept form:

The two points I found from the following graph are:

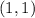`( 1, 1)` and
`(2, -2)`

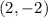
Trick: Since the line of the graph shows that it is down (not up), Start counting down from point
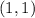`( 1, 1)` to point
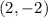`(2, -2)`. Then, find the y-intercept:

`m = (-3)/(1) = -3`

`b = 4`

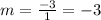
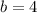
Use it to create a slope-intercept form:

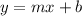`y = mx +b` (where
`m` represents the slope and
`b` represents the y-intercept)

`y = -3x +4`

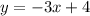
So, therefore the slope-intercept form is
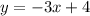`y = -3x +4` .