Answer:
1. The equation represent an exponential decay
2. The rate of the exponential decay is -3×2.5ˣ·㏑(2.5)
Explanation:
When a function a(t) = a₀(1 + r)ˣ has exponential growth, the logarithm of x grows with time such that;
log a(t) = log(a₀) + x·log(1 + r)
Hence in the equation -3 ≡ a₀, (1 + r) ≡ 2.5 and y ≡ a(t). Plugging in the values in the above equation for the condition of an exponential growth, we have;
log y = log(-3) + x·log(2.5)
Therefore, since log(-3) is complex, the equation does not represent an exponential growth hence the equation represents an exponential decay.
The rate of the exponential decay is given by the following equation;
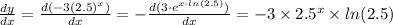
Hence the rate of exponential decay is -3×2.5ˣ × ㏑(2.5)