Question

The equation of a circle is given by (x + 3.5) ^ 2 + (y - 2.82) ^ 2 = 25 What is the area of a 52 degrees sector of this circle? Round to the nearest hundredth of a square unit.

Answer 1

≈ 11.34 units²

Explanation:

The equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k) are the coordinates of the centre and r is the radius

(x + 3.5)² + (y - 2.82)² = 25 ← is in standard form

with r² = 25 ⇒ r =
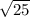`√(25)` = 5

The area (A) of the sector is calculated as

A = area of circle × fraction of circle

= πr² ×
`(52)/(360)`

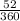
= π × 5² ×
`(52)/(360)`

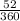
= π × 25 ×
`(52)/(360)`

=
`(25(52)\pi )/(360)`

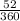
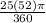
≈ 11.34 units² ( to the nearest hundredth )