Answer:
Point B must be at the same distance from the the origin as point A.
Explanation:
Coordinates of point A = (3, 3)
When point A is rotated 90° counterclockwise around the origin, coordinates of the new point B will be (-3, 3)
Distance from origin to point A =
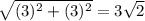
Similarly, distance of point B from the origin =
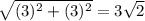
Therefore, distances of both the points from the origin are same.
Point B must be at the same distance from the the origin as point A.