Question

In how many ways can a

recorder, facilitator, and
questioner be chosen in a club
containing 14 members?

Answer 1

The answer is 364. There are 364 ways of choosing a recorder, a facilitator and a questioner froma club containing 14 members.

This is a Combination problem.

Combination is a branch of mathematics that deals with the problem relating to the number of iterations which allows one to select a sample of elements which we can term "r" from a collection or a group of distinct objects which we can name "n". The rules here are that replacements are not allowed and sample elements may be chosen in any order.

Explanation:

Step I

The formula is given as

`C (n,r) = (n)/(r) = (n!)/((r!(n-r)!))`

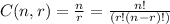
n (objects) = 14

r (sample) = 3

Step 2 - Insert Figures

C (14, 3) =
`((14)/(3))` =
`(14!)/((3!(14-3)!))`

=
`(87178291200)/((6 X 39916800))`

=
`(87178291200)/(239500800)`

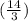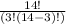
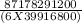
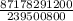
= 364

Step 3

The total number of ways a recorder, a facilitator and a questioner can be chosen in a club containing 14 members therefore is 364.

Cheers!