Question

Tin atoms are introduced into an FCC copper ,producing an alloy with a lattice parameter of 4.7589×10-8cm and a density of 8.772g/cm3 .Cal the atomic percentage of tin present in the alloy

Answer 1

atomic percentage = 143 %

Step-by-step explanation:

Let x be the number of tin atoms and there are 4 atoms / cell in the FCC structure , then 4 -x be the number of copper atoms . Therefore, the value of x can be determined by using the density equation as shown below:

`\mathbf{density (\rho) = ((no \ of \ atoms/cell)(atomic \ mass ))/((lattice \ parameter )^3(6.022*10^(23) atoms/ mol)) }`

where;

the lattice parameter is given as : 4.7589 × 10⁻⁸ cm

The atomic mass of tin is 118.69 g/mol

The atomic mass of copper is 63.54 g/mol

The density is 8.772 g/cm³

`\mathbf{8.772 g/cm^3 = ((x)(118.69 \ g/mol) +(4-x)(63.54 \ g/mol))/((4.7589*10^(-8) cm )^3(6.022*10^(23) atoms/ mol)) }`

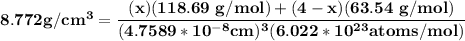
569.32 = 118.69x + 254.16-63.54x

569.32 - 254.16 = 118.69x - 63.54 x

315.16 = 55.15x

x = 315.16/55.15

x = 5.72 atoms/cell

As there are four atoms per cell in FCC structure for the metal, thus, the atomic percentage of the tin is calculated as follows :

atomic % =
`(no \ of \ atoms \ per \ cell \ in \ tin )/(no \ of \ atoms \ per \ cell \ in \ the \ metal)*100`

atomic % =
`(5.72 \ atoms / cell)/(4 \ atoms/ cell) *100`

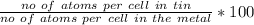
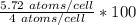
atomic % = 143 %