Question

Let f (x) = 3x − 1 and ε > 0. Find a δ > 0 such that 0 < ∣x − 5∣ < δ implies ∣f (x) − 14∣ < ε. (Find the largest such δ.) What limit does this prove?

Answer 1

This proves that f is continous at x=5.

Explanation:

Taking f(x) = 3x-1 and
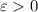`\varepsilon>0`, we want to find a
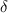`\delta` such that
`|f(x)-14|<\varepsilon`

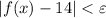
At first, we will assume that this delta exists and we will try to figure out its value.

Suppose that
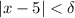`|x-5|<\delta`. Then

`|f(x)-14| = |3x-1-14| = |3x-15|=|3(x-5)| = 3|x-5|< 3\delta`.

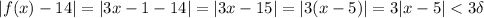Then, if
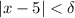`|x-5|<\delta`, then
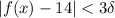`|f(x)-14|<3\delta`. So, in this case, if
`3\delta \leq \varepsilon` we get that
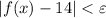`|f(x)-14|<\varepsilon`. The maximum value of delta is
`(\varepsilon)/(3)`.

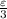By definition, this procedure proves that
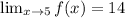`\lim_(x\to 5)f(x) = 14`. Note that f(5)=14, so this proves that f is continous at x=5.