Question

In the figure, b and c are parallel lines. Which of the following statements are true?

1.Joe claims the measure of angle 3 is equal to 90 degrees.Is he correct?why or why not
2.state the measure of angle 5 and how you know

Thank you!

Answer 1

1. No, Joe is not correct

2.
`\angle 5=72^(\circ)`

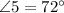
Explanation:

Given: b and c are parallel lines

To find:

1. whether the given statement is correct or not

2.
`\angle 5`

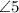
Solution:

1.

Sum of two angles that form a linear pair is equal to
`180^(\circ)`

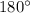
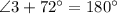`\angle 3+72^(\circ)=180^(\circ)` (linear pair)

`\angle 3=180^(\circ)-72^(\circ)=108^(\circ)\\eq 90^(\circ)`

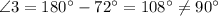
So, Joe is not correct

2.

If two lines are parallel then alternate interior angles are equal.

As b and c are parallel lines,

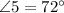`\angle 5=72^(\circ)` (alternate interior angles)