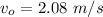Answer:
Step-by-step explanation:
From the question we are told that
The length of the wire is
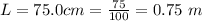
The mass of the wire is
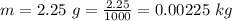
The tension is
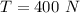
The frequency of the beat heard by the second student is
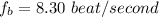
The speed of the wave generated by the vibration of the wire is mathematically represented as
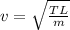
substituting values

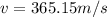
The wire is vibrating in its third harmonics so the wavelength is
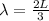
substituting values
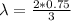
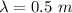
The frequency of this vibration is mathematically represented as
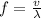
substituting values
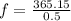

The speed of the second student (Observer) is mathematically represented as
![v_o = [(f_b)/(2f) ] * v](https://img.qammunity.org/2021/formulas/physics/college/rcfgeqyfufgmizkh0njfgg2lbxnazmorzy.png)
substituting values
![v_o = [(8.30)/(2* 730.3) ] * 365.15](https://img.qammunity.org/2021/formulas/physics/college/rsudr6wnev1s2aazom3h6329at824lp0mn.png)