Question

The number of milligrams of a drug in a person’s body after t hours is given by the function f(t) = 10e-0.3t. When will the amount of the drug be approximately 0.2 milligrams?

Answer 1

13 hours

Explanation:

right on edmentum

Answer 2

amount of the drug becomes approximately equal to 0.2 milligrams after 13.04 hours

Explanation:

Given: The function
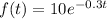`f(t)=10e^(-0.3 t)` represents number of milligrams of a drug in a person’s body after t hours

To find: time after which amount of the drug becomes approximately 0.2 milligrams

Solution:

`f(t)=10e^(-0.3 t)\\0.2=10e^(-0.3 t)\\(0.2)/(10)=e^(-0.3 t)\\(2)/(100)=e^(-0.3 t)\\(1)/(50)=e^(-0.3 t)\\`

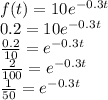
As
`e^x=y\Rightarrow x=\ln y` ,

`50=e^(0.3 t)\\0.3t=\ln 50\\t=(\ln 50)/(0.3)=13.04\,\,hours`

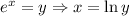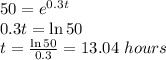
So, amount of the drug becomes approximately equal to 0.2 milligrams after 13.04 hours