Explanation:
Step 1: Answer question 1
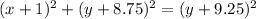
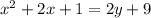
What we are doing in this problem, is that we are squaring both sides in order to help simplify. Number 1 has the second option or B.
Step 2: Answer question 2
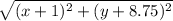
What we are doing is that we are finding the distance from the point on the parabola to the directrix. Number 2 has the last option or F.
Step 3: Answer question 3
Use (x, y)
What we are doing is that we are finding a point on a parabola. Number 3 has the fifth option or E.
Step 4: Answer question 4
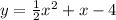
What we are doing is that we are writing the equation of the parabola. Number 4 has the third option or C.
Step 5: Answer question 5
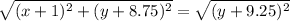
What we are doing is that we are setting the distance from focus to the point equal to the distance from directrix. Number 5 has the first option or A.
Step 6: Answer question 6
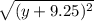
What we are doing is that we are finding the distance from the point on the parabola to the directrix . Number 5 has the fourth option or D.