Answer:
60
Explanation:
The function for the total profit is going to be
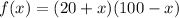 because the profit is the number of paintings multiplied by the number of dollars per painting, and for each additional painting the cost goes down by one. Multiplying this out, you get the quadratic function
because the profit is the number of paintings multiplied by the number of dollars per painting, and for each additional painting the cost goes down by one. Multiplying this out, you get the quadratic function
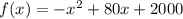 . We are trying to find the maximum, or the vertex, and we do not care about the y-coordinate of the vertex, which is the dollar amount, we only care about the x coordinate. We can find the x coordinate by using
. We are trying to find the maximum, or the vertex, and we do not care about the y-coordinate of the vertex, which is the dollar amount, we only care about the x coordinate. We can find the x coordinate by using
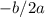 , which gives -80/-2 or 40. Now, we must remember that we started with 20 paintings, so adding 20 to 40 we get 60, the final answer.
, which gives -80/-2 or 40. Now, we must remember that we started with 20 paintings, so adding 20 to 40 we get 60, the final answer.