Question

Which of the following are characteristics of the graph of the square root

parent function? Check all that apply.
A. It has a domain of x 0.
B. It has a range of yz 0.
O c. It starts at the origin.
D. It is a straight line.

Answer 1

Choices A and B have typos in them, so its not clear what you're trying to say for those parts. However, the domain of
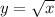`y = √(x)` is
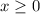`x \ge 0` meaning that x can be 0 or larger. In other words, we can't have x be negative. Similarly, y is the same story because
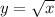`y = √(x)` has the inverse
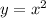`y = x^2`, but only when
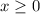`x \ge 0`, so therefore
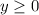`y \ge 0` as well. In short you can say both x and y are nonnegative.

To summarize so far, the domain is
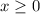`x \ge 0` and the range is
`y \ge 0`

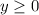
Since x = 0 and y = 0 are the smallest x and y values possible, this means (x,y) = (0,0) is the left-most point or where the graph starts. This is the origin. Choice C is a true statement.

Choice D on the other hand is not a true statement. Graph out
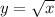`y = √(x)` and you'll see that a straight line does not form, but instead a nonlinear curve that grows forever. That growth gradually diminishes as x gets larger. Algebraically you can pick three points from the function and show that the slopes are different. Say the three points are P, Q and R. If you can show that slope of PQ does not equal slope of QR, then the function is not linear.