To find the tangent line of the graph:
⇒ must find:
- point at which the tangent line touches the graph
- slope of the tangent line
Let's find the point at which the tangent line touches the graph:
At x = -1,
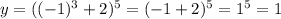
Point: (-1,1)
Let's find the slope of the tangent line
⇒ get the derivation of function than plug (-1) in the x-position to get
the exact slope
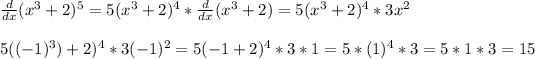
Slope of tangent line: 15
Now put all the calculated value into the point-slope form:
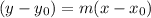
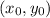 --> point on the tangent line
--> point on the tangent line- m --> tangent slope's value
So:
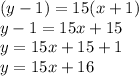
Thus the tangent line's equation is y = 15x + 16
Answer: y = 15x + 16
Hope that helps!