Question

5) Two machines M1, M2 are used to manufacture resistors with a design

specification of 1000 ohm with 10% tolerance. Resistors of M1 are found to
follow normal distribution with mean 1050 ohm and standard deviation of 100
ohm, while those of M2 are found to follow normal distribution with mean 1000
ohm and standard deviation of 120 ohm. Which machine do you prefer? Why?​

Answer 1

Since M1 has the higher probability of being in the desired range, we choose M1.

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Two machines M1, M2 are used to manufacture resistors with a design specification of 1000 ohm with 10% tolerance.

So we need the machines to be within 1000 - 0.1*1000 = 900 ohms and 1000 + 0.1*1000 = 1100 ohms.

For each machine, we need to find the probabilty of the machine being in this range. We choose the one with the higher probability.

M1:

Resistors of M1 are found to follow normal distribution with mean 1050 ohm and standard deviation of 100 ohm. This means that
`\mu = 1050, \sigma = 100`

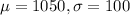
The probability is the pvalue of Z when X = 1100 subtracted by the pvalue of Z when X = 900. So

X = 1100

`Z = (X - \mu)/(\sigma)`

`Z = (1100 - 1050)/(100)`

`Z = 0.5`

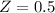
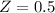`Z = 0.5` has a pvalue of 0.6915.

X = 900

`Z = (X - \mu)/(\sigma)`

`Z = (900 - 1050)/(100)`

`Z = -1.5`

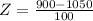
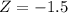
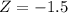`Z = -1.5` has a pvalue of 0.0668

0.6915 - 0.0668 = 0.6247.

M1 has a 62.47% probability of being in the desired range.

M2:

M2 are found to follow normal distribution with mean 1000 ohm and standard deviation of 120 ohm. This means that
`\mu = 1000, \sigma = 120`

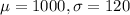
X = 1100

`Z = (X - \mu)/(\sigma)`

`Z = (1100 - 1000)/(120)`

`Z = 0.83`

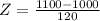
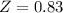
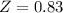`Z = 0.83` has a pvalue of 0.7967.

X = 900

`Z = (X - \mu)/(\sigma)`

`Z = (900 - 1000)/(120)`

`Z = -0.83`

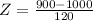
`Z = -0.83` has a pvalue of 0.2033

0.7967 - 0.2033 = 0.5934

M2 has a 59.34% probability of being in the desired range.

Since M1 has the higher probability of being in the desired range, we choose M1.