We have been given graph of a sinusoidal function. We are asked to write function formula for our given graph.
We know that
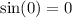 and
and
 . We can see that our given function is starting at origin, so our graph is sine function.
. We can see that our given function is starting at origin, so our graph is sine function.
We know that general form of sine is
![y=A\sin[B(x-c)]+D](https://img.qammunity.org/2021/formulas/mathematics/high-school/oylnk7hm2vlyxsxx80ls97cg90bv8pdpe8.png) , where,
, where,
A = Amplitude,
Period:
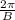
C = Horizontal shift,
D = Vertical shift.
We have been given that function has no horizontal shift, so the value of C is 0.
We can also see that midline of our function is x-axis, so there is no vertical shift as well that is
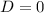 .
.
We can see that function goes up to 1 from midline and goes down to
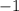 from midline, so amplitude of function is 1 that is
from midline, so amplitude of function is 1 that is
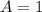 .
.
We can see that period of our given function is
 because it completes one cycle from
because it completes one cycle from
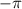 to
to
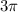

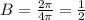

We can see that our function is reflected about x-axis, so our function will be
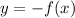 .
.
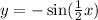
Therefore, our required function is
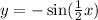 .
.