Question

Suppose that Matthew can choose to get home from work by car or bus.

When he chooses to get home by car, he arrives home after 7 p.m. 6 percent of the time.
When he chooses to get home by bus, he arrives home after 7 p.m. 25 percent of the time.
Because the bus is cheaper, he uses the bus 70 percent of the time.
What is the approximate probability that Matthew chose to get home from work by bus, given that he arrived home after 7 p.m.?

A-70%
B-91%
C-18%
D-20%

Answer 1

B-91%

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

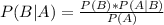
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: arriving home after 7 p.m.

Event B: getting home by bus.

When he chooses to get home by bus, he arrives home after 7 p.m. 25 percent of the time.

This means that
`P(A|B) = 0.25`

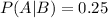
Because the bus is cheaper, he uses the bus 70 percent of the time.

This means that
`P(B) = 0.7`

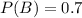
Probability of getting home after 7 p.m.

70% of the time he uses bus, and by bus, he arrives arrives home after 7 p.m. 25 percent of the time.

100 - 70 = 30% of the time he uses the car, and by car, he arrives home after 7 p.m. 6 percent of the time.

So

`P(A) = 0.7*0.25 + 0.3*0.06 = 0.193`

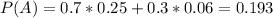
What is the approximate probability that Matthew chose to get home from work by bus, given that he arrived home after 7 p.m.?

`P(B|A) = (0.7*0.25)/(0.193) = 0.9067`

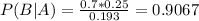
Rouding up, 91%.

So the correct answer is:

B-91%