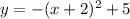Answer:
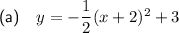


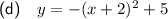
Explanation:
Vertex form

where (h, k) is the vertex
-------------------------------------------------------------------------------------------
Part (a)
Given: vertex at (-2, 3) passes through (-4 ,1)
Substituting the given vertex into the equation:
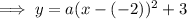
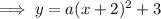
Substitute the given point into the equation to find a:

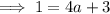
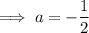
Substitute the found value of a to form the final equation:
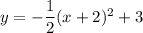
-------------------------------------------------------------------------------------------
Part (b)
Given: vertex at (-1, -1) passes through ?)
Substituting the given vertex into the equation:
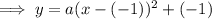
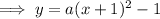
Substitute the given point into the equation to find a:
**no point given**
-------------------------------------------------------------------------------------------
Part (c)
Given: vertex at (-2, -3) passes through (-5, 6)
Substituting the given vertex into the equation:


Substitute the given point into the equation to find a:

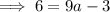
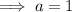
Substitute the given point into the equation to find a:
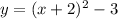
-------------------------------------------------------------------------------------------
Part (d)
Given: vertex at (-2, 5) passes through (1, -4)
Substituting the given vertex into the equation:
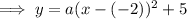

Substitute the given point into the equation to find a:
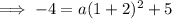
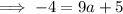
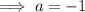
Substitute the given point into the equation to find a: